Answer:
The solutions of the system are
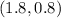 and
and
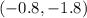 .
.
Explanation:
The given system is

This is nonlinear system of equations, notice that it's about the intersection between a circle and a line, which can be in one point (tangent) or in two points (secant).
Let's isolate
 in the second equation, and then we replace that expression into the first equation
in the second equation, and then we replace that expression into the first equation
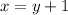
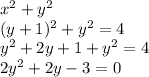
Using a calculator, the solutions are
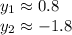
Now, we use these values, to find their pairs.
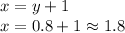
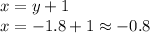
Therefore, the solutions of the system are
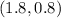 and
and
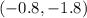 .
.
The image attached shows the solutions graphically.