Answer:
2x+y=0
Explanation:
Given:
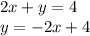
To find:
- The equation of line that’s parallel and passes through origin point.
Parallel Definition:
- Both lines have same slope.
Slope-Intercept:

Therefore, another line is:

Since the line passes through origin point which is (0,0). Substitute x = 0 and y = 0 in the equation:

Therefore, the equation is:
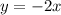
Convert back to standards form:
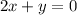
Therefore, another line that is parallel to
 is 2x+y=0
is 2x+y=0