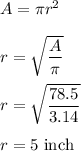Explanation:
Juan wants to know the cross-sectional area of a circular pipe. He measures the diameter which he finds, to the nearest millimetre, to be 5 centimetres
It means radius is 2.5 cm. For the area of circle he gets the formula as :
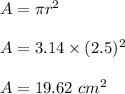
If Michelle found the area of a circle as
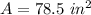
So,