Question

Sphere and a cylinder have the same radius and height. The volume of the cylinder is 64 meters cubed.

A sphere with height h and radius r. A cylinder with height h and radius r.

What is the volume of the sphere?
StartFraction 64 Over 3 EndFraction meters cubed
32 meters cubed
StartFraction 128 Over 3 EndFraction meters cubed
64 meters cubed

Answer 1

C. StartFraction 128 Over 3

Explanation:

Volume of cylinder:

Pi × r² × h

h = 2r

Pi × r² × 2r = 64

Pi × r³ = 32

Volume of sphere:

(4/3)pi × r³

(4/3)(32)

128/3

Answer 2

C. 128/3 meters cubed

Explanation:

The volume of a cylinder is denoted by:
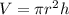`V=\pi r^2h`, where r is the radius and h is the height. We know it's equal to 64, so we can set that equal to V:

`V=\pi r^2h`

`64=\pi r^2h`

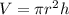
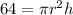
We know that the sphere and cylinder have the same height and radius. However, the "height" of a sphere is actually the same as its diameter, which is twice its radius. Then, we can replace h in the above equation with 2r:

`64=\pi r^2h`

`64=\pi r^2*2r=2\pi r^3`

`\pi r^3=64/2=32`

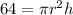
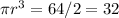
Now, the volume of a sphere is denoted by:
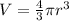`V=(4)/(3) \pi r^3`, where r is the radius. From above, we know that
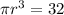`\pi r^3=32`, so we can plug this into the equation:

`V=(4)/(3) \pi r^3`

`V=(4)/(3) *32=128/3`

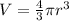
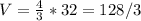
Thus, the answer is C.