Question

What is the sum? 3 y / Y 2 + 7 y + 10 + 2 / y + 2​

Answer 1

5/(y+5)

Explanation:

Perhaps you want the sum ...

`(3y)/(y^2+7y+10)+(2)/(y+2)\\\\=(3y)/((y+2)(y+5))+(2(y+5))/((y+2)(y+5))=(3y+2(y+5))/((y+2)(y+5))\\\\=(5y+10)/((y+2)(y+5))=(5(y+2))/((y+2)(y+5))=\boxed{(5)/(y+5)}`

_____

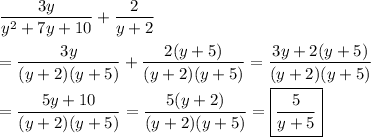
Comment on rational expressions

When writing ratios in plain text, it is imperative to put parentheses around numerators and denominators. (If the numerator is a product only, then parentheses are optional.)

Your expression might be properly written as ...

3y/(y^2 +7y +10) +2/(y+2)

As you have written it, it simplifies to ...

3(y/y)2 +7y +10 +2/y +2 = 3·2 +7y +2/y +12

= 7y +2/y +18

Please note, too, the exponentiation symbol (^).