Question

I need help ASAP (only have five minutes)

The Saxena family plans to install a light to illuminate part of their rectangular yard. Nikki and Dylan each proposed a different spot to place the light. The proposed placements and the lit area that each produces are shown below.

Nikki's proposed placemat has a triangular light area with a base of 60 feet and a height of 38 feet. Dylan's proposed placemat has a base of 60 feet and a height of 38 feet.

How do Nikki’s and Dylan’s proposals compare? Check all that apply.

Nikki’s proposed placement will light a greater area than Dylan’s placement.

Dylan’s proposed placement will light a greater area than Nikki’s placement.

Both proposed placements will light the same sized area.

Nikki’s proposed placement will light more than half the yard.

Dylan’s proposed placement will light more than half the yard.

Dylan’s proposed placement will light exactly half of the yard.

Nikki’s proposed placement will light less than half of the yard.

Answer 1

(C)Both proposed placements will light the same sized area.

(F)Dylan’s proposed placement will light exactly half of the yard.

Explanation:

The diagram of the proposed light placement is reproduced and attached.

Area of the Rectangular Yard=60 X 38=2280 Square feet

The lit area for both placement is in a triangular shape.

`\text{Area of a triangle=}(1)/(2)bh`

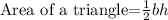
Area of Nikki's Proposed Placement Lit Area
`=(1)/(2)*60*38=1140 \: Square \:feet`

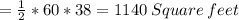
Area of Dylan's Proposed Placement Lit Area
`=(1)/(2)*60*38=1140 \: Square \:feet`

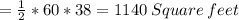
Therefore, the following options are correct:

(C)Both proposed placements will light the same sized area.

(F)Dylan’s proposed placement will light exactly half of the yard.