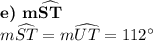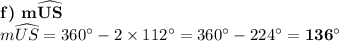Question

In circle Z, if vz = zw, sv=21, and mUT=112degrees, find each measure

Answer 1

A) UT = 42; WT = 21; ST = 42

`\text{d) } m\widehat {XT} = 56^(\circ); \text{e) } m\widehat {ST} = 112^(\circ); \text{f) }m\widehat {US} = 136^(\circ)`

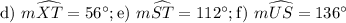
Explanation:

a), b), and c)

YZ ⟂ ST, so SV = TV = 21

In ∆s ZVT and ZWT,

∠ZVT = ∠ZWT; ZV = ZW; ZT is common.

∴ ∆ZVT ≅ ∆ZWT

∴ ∠ZTV = ∠ZTW

In ∆s SVZ and TVZ,

SV = TV; SZ = TZ; VZ is common

∴ ∆SVZ ≅ ∆TVZ

∴ ∠SZV = ∠TZV

By similar reasoning,

∆TWZ ≅ ∆UWZ

∴ ∠TZW = ∠UZW

So, the four angles marked with red dots are equal.

Also, SV = TV = TW = UW = 21

In ∆s STZ and UTZ,

SZ = UZ; ST =UT; TZ is common

∴ ∆STZ ≅ ∆UTZ

∴ ∠SZT = ∠UZT and

ST = UT = 42

`\textbf{e) m} \mathbf{\widehat {ST}}\\m \widehat {ST} =m \widehat {UT } = 112^(\circ)`

`\textbf{d) m} \mathbf{\widehat {XT}}\\m \widehat {XT} = (1)/(2) m \widehat {UT } = (1)/(2)(112^(\circ)) = \mathbf{56^(\circ)}`

`\textbf{f) m} \mathbf{\widehat {US}}\\m\widehat {US} =360^(\circ) - 2* 112^(\circ) = 360^(\circ) - 224^(\circ) = \mathbf{136^(\circ)}`