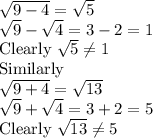Answer:
(C)The square root of terms separated by addition and subtraction cannot be calculated individually.
Explanation:
In Step 7:
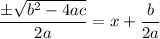
The expression
 cannot be written as
cannot be written as
 . This is as a result of the fact that square roots of terms separated by addition and subtraction cannot be calculated individually.
. This is as a result of the fact that square roots of terms separated by addition and subtraction cannot be calculated individually.
Take these examples: