Question

Does this converge or diverge? Which of the follow test will be used to figure out the equation?

1+1/root(2)+1/root(3)+1/root(4)+...
A. Intergal test
B. P-series
C. Geometric Series
D. Nth term test for Divergency

Answer 1

From the listed choices, you can prove the series diverges using either the integral or p-series test.

• Integral test:

We have

`\displaystyle\sum_(n=1)^\infty\ge\int_1^\infty(\mathrm dx)/(\sqrt x)=\lim_(x\to\infty)2\sqrt x-2`

which diverges to infinity, so the series is divergent.

• p-series test:

The series

`\displaystyle\sum_(n=1)^\infty\frac1{n^p}`

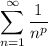
converges only for
`p>1`. In the given sum, we have
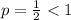`p=\frac12<1`, so the series is divergent.