Answer:
x = 4
Explanation:
When you have a coefficent in front of a logarithm function, you can take the argument to the power of that coefficient. For example, the 3 in front of the logarithm can be brought into the argument, and you can take 'x' to the third power. You get:
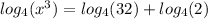
When you add logarithms, it is equivalent to multiplying their arguments:
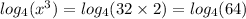
Since both sides are log base 4, the arguments must equal each other:
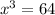
![x = \sqrt[3]{64} = 4](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/di8dynpa3y4tiref5l0l.png)