Question

Test each following to convergance

∑(n=1,∞)(√(n^3 +5n -1)/(n^2 - sin(n^3))


2. the sequence { (n^2 /(3*n +1 ))sin ((\pi[/tex])/(3*n ) } for all n≥1


pi =3.14.

Answer 1

1. Compare the series to the divergent p-series,

`\displaystyle\sum_(n=1)^\infty\frac1{\sqrt n}`

Use the limit comparison test: we have

`\displaystyle\lim_(n\to\infty)\frac{(√(n^3+5n-1))/(n^2-\sin(n^3))}{\frac1{\sqrt n}}=1`

so the given series also diverges.

Breakdown for the limit:
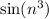`\sin(n^3)` oscillates between -1 and 1, so its contribution to the denominator
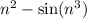`n^2-\sin(n^3)` is neglible and we can replace it with
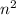`n^2`. In the square root in the numerator, the
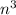`n^3` term dominates, so
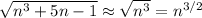`√(n^3+5n-1)\approx√(n^3)=n^(3/2)`. So the given summand is approximated by

`(n^(3/2))/(n^2)=\frac1{n^(1/2)}=\frac1{\sqrt n}`

2. Let
`m=\frac\pi{3n}`, so that
`m\to0` as
`n\to\infty`. Then

`\displaystyle\lim_(n\to\infty)(n^2)/(3n+1)\sin\left(\frac\pi{3n}\right)=\lim_(m\to0)((\pi^2)/(9m^2))/(\frac\pi m+1)\sin m`

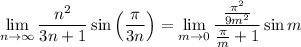
Recall that
`\frac{\sin x}x\to1` as
`x\to0`. Rewrite the limit as

`\displaystyle\lim_(m\to0)\frac{\frac{\pi^2}9}{m+\pi}\frac{\sin m}m`

Then
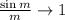`\frac{\sin m}m\to1`, and we're left with

`\displaystyle\lim_(m\to0)\frac{\frac{\pi^2}9}{m+\pi}`

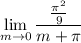
which is continuous at
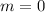`m=0`, giving a limit of
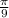`\frac\pi9`.