Answer: x = 64
Explanation:
First you need to know that if we have:
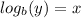 this is equal to
this is equal to
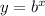
So,
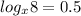 can be rewritten as:
can be rewritten as:
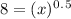
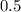 can be rewritten as:
can be rewritten as:
 and why did I do this? you may ask. This way I can rewrite the exponent as a square root, as following;
and why did I do this? you may ask. This way I can rewrite the exponent as a square root, as following;
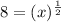
The property says that:
![\sqrt[n]{x^m}=x^(m)/(n)](https://img.qammunity.org/2021/formulas/mathematics/middle-school/vyfnvvcpnve1vix48xvw8nl2bss4uau2ib.png)
So, we can rewrite our operation as;
![8=\sqrt[]{x}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/u4uwjggt46sxkr7fo5efnkapla7d2nkppv.png)
Now let's raise both sides to the power of 2, to get rid of the square root.
![(8)^2=(\sqrt[]{x})^2](https://img.qammunity.org/2021/formulas/mathematics/middle-school/1zmdceec6gmi18slk5vbo1ozcnmqqen29v.png)
