Answer:
4294967293 dots
Explanation:
Figure 1 has 5 dots.
Figure 2 has 13 dots.
Figure 3 has 29 dots.
Subtract and find different of each term:
Let
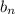 be sequence of difference (and the sequence appears to be geometric.)
be sequence of difference (and the sequence appears to be geometric.)
So for
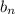 , find the common ratio which is 2.
, find the common ratio which is 2.
Hence,
 - recall geometric sequence formula below:
- recall geometric sequence formula below:
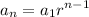
The sequence of difference
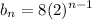 can be simplified to:
can be simplified to:
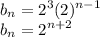
Now to find the original sequence:
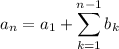
Hence:

Recall:
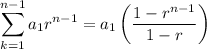
Therefore:
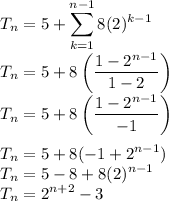
Therefore, the sequence for 5,13,29 is
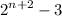 .
.
Therefore, in figure 30:
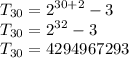
Therefore, there are 4294967293 dots in figure 30