Question

Show that the derivative of an odd function is even function and viceversal​

Answer 1

Explanation:

Well, it's hard to generalize this. But I can show you a few examples using the power rule and some derivatives of trig functions. Lets say we have a function:

`f(x) = {x}^(n)`

Then you should know it's derivative is:

`(df)/(dx) = n {x}^(n - 1)`

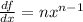
For polynomial functions, a subtraction of 1 from the exponent will turn any odd function into an even, and any even function to an odd. An example of this is x^3, which is odd. The derivative is 3x^2, which is even. Another example, this time of a trig function, is sine and cosine. Sine is odd, while cosine is even. The derivative of sine is cosine, and the derivative of cosine is negative sine.