Answer:
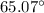
Step-by-step explanation:
The critical angle in oil for the oil-water interface refers to the angle for which the light ray is totally reflected.
Angle of incidence = 73.4°
Angle of refraction = 1.470°
Index of refraction = 1.333
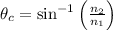
Here,
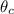 refers to the critical angle.
refers to the critical angle.
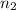 is an index of refraction
is an index of refraction
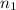 is angle of refraction
is angle of refraction
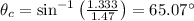
Here, angle of incidence is more than the critical angle,
light undergoes total internal reflection.