Question

You have a beaker with a layer of olive oil floating on top of water. A ray of light travels through the oil and is incident on the water with an angle of 73.4°. Using the index of refraction of the oil as 1.470 and the index of refraction of water as 1.333, determine the critical angle in oil for the oil-water interface.

Answer 1

`65.07^(\circ)`

Step-by-step explanation:

The critical angle in oil for the oil-water interface refers to the angle for which the light ray is totally reflected.

Angle of incidence = 73.4°

Angle of refraction = 1.470°

Index of refraction = 1.333

`\theta_c=\sin^(-1)\left ( (n_2)/(n_1) \right )`

Here,
`\theta_c` refers to the critical angle.

`n_2` is an index of refraction

`n_1` is angle of refraction

`\theta_c=\sin^(-1)\left ( (1.333)/(1.47) \right )=65.07^(\circ)`

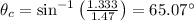
Here, angle of incidence is more than the critical angle,

light undergoes total internal reflection.