Answer:

Explanation:
Let's start by finding the common difference of this arithmetic sequence.
The change from
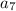 to
to
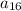 is -45 because it decreased 45.
is -45 because it decreased 45.
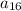 is 9 terms away from
is 9 terms away from
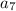 .
.
If we divide the change by the difference in n, then we can find the difference between each term, or the common difference.
-45/9 = -5, so the common difference is -5.
Now, we want to find
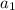 .
.
We can do this using the common difference. Subtracting the common difference from
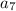 six times should tell us what
six times should tell us what
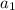 is, so let's do that.
is, so let's do that.
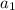 = 71 - (-5) - (-5) - (-5) - (-5) - (-5) - (-5)
= 71 - (-5) - (-5) - (-5) - (-5) - (-5) - (-5)
A reminder, subtracting a negative is basically the same as adding it.
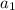 = 71 + 5 + 5 + 5 + 5 + 5 + 5
= 71 + 5 + 5 + 5 + 5 + 5 + 5
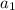 = 101
= 101
With the common difference and
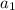 , we now have all the parts we need to write a rule for the nth term of this sequence.
, we now have all the parts we need to write a rule for the nth term of this sequence.
The formula for the nth term of a sequence is
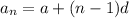 , with
, with
 being the nth term, a being
being the nth term, a being
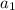 , and d being the common difference.
, and d being the common difference.
We can just substitute the common difference and a to get our formula.
