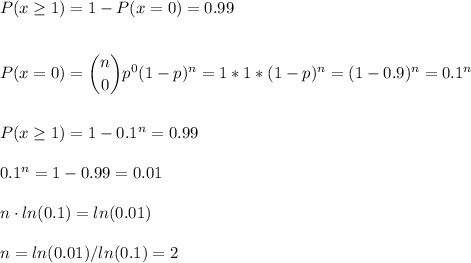Question

A variation on a familiar theme: A packet is received correctly by an end user with probability p. To increase the likelihood that an important message is received, the packet is sent repeatedly N times. Let random variable X be the number of copies received correctly by the end user. a) Find the PMF PX(x). b) If p = 0.9, how large should N be to ensure that with probability 0.99 at least one copy of the message is received

Answer 1

Answer : N=2

Explanation:

X: R.V denoting # copies received correctly,

so, X = Bin (N,P)

= P (X-x) = (N/x) p× (1-p)N-x x=0,1,2 .............

(b) p= 0.9

p(X, 7, 1) = 0.99

1- P (X=0) = 0.99

P(X=0) = 0.01

(0.01)N = 0.01

N=2

Answer 2

a) X can take the values {0,1,2,3,...,n}

The probability mass function of x is defined for k copies received correctly as:

`P(X=k)=\dbinom{n}{k}p^k(1-p)^(n-k)`

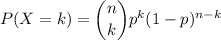
b) N should be N=2 to ensure that with probability 0.99 at least one copy of the message is received.

Explanation:

The variable X:number of copies received correctly by the end user can be modeled as a binomial variable, as it is a sum of n Bernoulli variables with probability p.

X can take the values {0,1,2,3,...,n}

The probability mass function of x is defined for k copies received correctly as:

`P(X=k)=\dbinom{n}{k}p^k(1-p)^(n-k)`

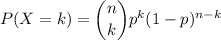
being p: the probability that a packet is received correctly by an end user, and q=1-p: the probability that a packet is not received correctly by an end user.

b) We have to calculate n so as to have a probability P(x≥1)=0.99, when p=0.9.

`P(x\geq1)=1-P(x=0)=0.99\\\\\\P(x=0)=\dbinom{n}{0}p^0(1-p)^n=1*1*(1-p)^n=(1-0.9)^n=0.1^n\\\\\\P(x\geq1)=1-0.1^n=0.99\\\\0.1^n=1-0.99=0.01\\\\n\cdot ln(0.1)=ln(0.01)\\\\n=ln(0.01)/ln(0.1)=2`