Question

A sector Whos radius is 10 feet, has an area of 200pi/9 ft squared. What are the measures of the central and inscribed angels for this sector?

Answer 1

`\theta=(4\pi)/(9)` .

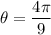Explanation:

Given information:

Radius = 10 feet

Area =
`(200\pi)/(9)` sq. ft. ...(i)

We need to find the measures of the central and inscribed angels for this sector.

The area of a sector is

`A=(1)/(2)r^2\theta`

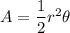
where, r is radius and
`\theta` is central angle in radian.

Substitute r = 10 in the above formula.

`A=(1)/(2)(10)^2\theta`

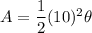
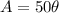`A=50\theta` ...(ii)

From (i) and (ii), we get

`50 \theta=(200\pi)/(9)`

`\theta=(200\pi)/(9* 50)`

`\theta=(4\pi)/(9)`

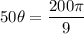
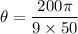
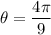
Therefore, the measure of central angle is
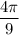`(4\pi)/(9)`.