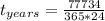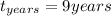Question

A piece of corroded steel plate was found in a submerged ocean vessel. It was estimated that the original area of the plate was 11 in.2 and that approximately 2.3 kg had corroded away during the submersion. Assuming a corrosion penetration rate of 200 mpy for this alloy in seawater, estimate the time of submersion in years. The density of steel is 7.9 g/cm3.

Answer 1

The time of the submersion is
`t_(years) = 9 years`

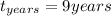
Step-by-step explanation:

From the question we are told that

The area of the plate is
`A = 11 in^2`

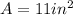
The mass of the corroded plate
`m = 2.3 \ kg = 2.3 * 1*10^(6)= 2.3 *10^(6) mg`

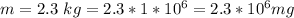
The corrosion penetration rate is
`R = 200 mpy`

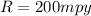
The density of steel is
`\rho = 7.9 g/cm^3`

Generally the corrosion penetration rate can be mathematically represented as

`R = (K m)/(A \rho t)`

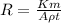
Where K is the corrosion imperial unit constant whose value is K = 534 mpy

t is the exposure time of the plate

Making t the subject of the formula

`t = (K m)/(R \rho A)`

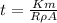
Substituting value

`t = (534 *2.3*10^(6))/(200 * 7.9 * 10 )`

`t = 77734 hrs`

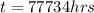
Converting to years

`t_(years) = (77734)/(365 * 24)`

`t_(years) = 9 years`