Question;
It is said that happy and healthy workers are efficient and productive. A company that manufactures exercising machines wanted to know the percentage of large companies that provide on-site health club facilities. A sample of 200 such companies showed that 150 of them provide such facilities on site.
What is the point estimate of the percentage of all such companies that provide such facilities on site and Construct a 98% confidence interval for the percentage of all such companies that provide such facilities on site as well as find the margin of error for this estimate?
Answer:
Confidence interval is 0.7 ≤ p ≤ 0.8
The margin of error is 7.1 %
Explanation:
Here we have, the proportion or point estimate given by
 = 150/200 = 0.75
= 150/200 = 0.75
Sample size, n = 200
The formula for confidence interval, CI, given a proportion is;
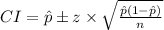
At 98% z = ±2.326348
Plugging in the values of
 , z and n we get;
, z and n we get;
CI = 0.6787704 ≤ p ≤ 0.8212296
To one decimal place, we have
CI = 0.7 ≤ p ≤ 0.8
The margin of error =
 , plugging in the values of
, plugging in the values of
 , z and n we get;
, z and n we get;
The margin of error = 0.0712296 = 7.12296%
The margin of error = 7.1 % to one decimal place.