Question

What is the change ΔT in the period of a simple pendulum when the acceleration of gravity g changes by Δg? (Hint: The new period T+ΔT is obtained by substituting g+Δg for g: T+ΔT=2πLg+Δg−−−−√. To obtain an approximate expression, expand the factor (g+Δg)−1/2 using the binomial theorem and keep only the first two terms: (g+Δg)−1/2=g−1/2−12g−3/2Δg+⋯ The other terms contain higher powers of Δg and are very small if Δg is small.) Express your result as the fractional change in period ΔTT in terms of the fractional change Δgg.

Answer 1

`\Delta T=-\pi\sqrt{(l)/(g)}(\Delta g)/(g)`

Step-by-step explanation:

The period of a pendulum is given by the following formula:

`T=2\pi\sqrt{(l)/(g)}`

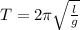
l: length of pendulum

g: gravity constant

If there is a little increase in g to g+Δg you have:

ΔT +
`T=2\pi\sqrt{(l)/(g+\Delta g)}=2\pi((l)^(1/2))/((g+\Delta g)^(1/2))=2\pi(l)^(1/2)(g+\Delta g)^(-1/2)`

by using the expansion for (g+Δg)^{-1/2} term you obtain:

`(g+\Delta g)^(-1/2)=(g)^(-1/2)(1+(\Delta g)/(g))^(-1/2)\\\\= (g)^(-1/2)[1-(1)/(2)(\Delta g)/(g)+(3)/(8)((\Delta g)/(g))^2+...]`

However, due to Δg is very lower in comparison with g, you can consider that (Δg/g)^2 ≈ 0 and also for higher exponents. Thus, you obtain for T:

`T+\Delta T=2\pi(l)^(1/2)(g)^(-1/2)[1-(1)/(2)(\Delta g)/(g)]=2\pi \sqrt{(l)/(g)}[1-(1)/(2)(\Delta g)/(g)]=2\pi\sqrt{(l)/(g)}-\pi\sqrt{(l)/(g)}(\Delta g)/(g)`

from the previous result you can conclude the following:

`\Delta T=-\pi\sqrt{(l)/(g)}(\Delta g)/(g)`