Answer:
- First number = 10
- Second number = 51
- Third number = 17
Explanation:
In the question we are given ,
- Sum of three numbers is 78
- Third no. is 7 more than first
- Second no. is 3 times third
So , we are assuming that ,
- Third no. be x + 7 ( because in question it is given that third number is 7 more than the first number ) .
- Second no. be 3 ( x + 7 ) ( because in the question it is given that second no. is three times the third )
We are finding the solution by adding all these term and equating it with 78 because sum of these three numbers is equal to 78 .
Here we go ,

Step 1 : Solving the bracket part :
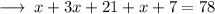
Step 2 : Adding like terms :
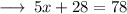
Step 3 : Transposing 28 to right hand side :
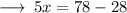
Step 4 : Subtracting 28 from 78 :
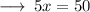
Step 5 : Transposing 5 to right hand side :
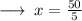
Step 6 ; Cancelling 50 with 5 :
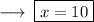
Therefore value of ,
- 3(x + 7 ) [ second number ] = 51
- x + 7 [ third number ] = 17
Verification :
We are verifying our answer by adding the three numbers and it must be equal to 78 .
Therefore , our answer is correct .
#Keep Learning