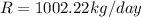Question

Wastewater from a primary treatment tank is to undergo secondary treatment in an activated sludge unit. The following data and operational parameters are specified: Two identical units are designed to operate in parallel and to process a combined wastewater flow rate of 0.5 m3 /s; the BOD5 of the effluent suspended solids is 70% of the allowable suspended solids concentration. Assume ideal operation of the reactor units. (a) If the EPA’s secondary treatment standards (average monthly) are to be met. How large must each reactor be (m3 )?

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

a

The volume of each reactor is
`V= 691.53\ m^3`

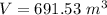
b

The rate at which cells must be discharged in the unit is
`R = 1002.22 kg/day`

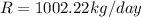
Step-by-step explanation:

From the question we are told that

The water flow rate of the units is
`\r q = 0.5 m^3/s`

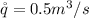
The
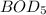`BOD_5`(Biochemical oxygen demand) of the effluent suspended solid is
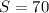`S = 70`% of allowable suspended solid concentration

Given that the flow rate for two identical parallel units then for a single unit the flow rate would be

`Q = (\r q)/(2) = (0.5)/(2) = 0.25 m^3 /s`

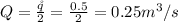
Generally the required BOD in terms of EPA(Effluent Guidelines) is concerned is
`S_e = 30 mg/l`

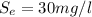
Now Sludge age of this unit of reactor is mathematically evaluated from this expression

`S_e = (k_s (1 + k_d \theta_c))/(\theta_c (\mu_m - k_d) - 1)`

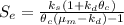
Where
`\theta_c` is the Sludge age

Substituting values

`30 = (30 (1 + 0.05 \theta_c))/(\theta_c (3 - 0.05) - 1)`

`30 = ( 30 + 1.5\theta_c))/(( 3 \theta_c - 0.05 \theta_c) - 1)`

=>
`\theta _ c = 0.69 \ days = 59616s`

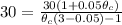
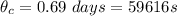
Now the volume of the reactor is mathematically evaluated from this relation

`VX = \frac{\r q Y (S_o - S) \theta_c} {1 - k_d \theta_c}`

Making V the subject of the formula

`V = \frac{\r q Y (S_o - S) \theta_c} {1 - k_d \theta_c} * (1)/(X)`

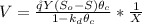
Substituting values

`V = (0.25 * 4 (150 - 30 ) * 59616 )/(1+ 0.05 * 0.69) * (1)/(1000)`

=>
`V= 691.53\ m^3`

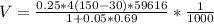
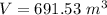
We can obtain the cell mass been wasted per day using this expression

`Q_w X_i = ((VX)/(\theta _c))kg /day`

Where
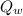`Q_w` is given as
`Q_w = 10 L/s = 10 *10^(-3) \ m^3 /s`

`Q_w X_i` is the sludge been wasted per day

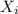`X_i` is the discharge concentration for each unit

Substituting values

`X_i Q_w = (1002.22)/(86400)`

`X_i = (1002.22)/(86400) * (1)/(10*10^(-3))`

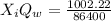
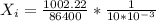
Now the rate at which they discharge this concentration is mathematically evaluated as

`R = X_i * Q_w * 86400`

substituting values

`R = 1002.22 kg/day`