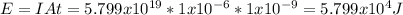Question

Lasers can be constructed that produce an extremely high intensity electromagnetic wave for a brief time—called pulsed lasers. They are used to ignite nuclear fusion, for example. Such a laser may produce an electromagnetic wave with a maximum electric field strength of 2.09\times 10^{11}~\text{V/m}2.09×10 ​11 ​​ V/m for a time of 1.00 ns. What energy does it deliver on a 1.00~\mathrm{mm^2}1.00 mm ​2 ​​ area?

Answer 1

The energy it delivers is 5.799x10⁴J

Step-by-step explanation:

Given data:

Em = maximum electric field = 2.09x10¹¹V/m

t = time = 1 ns = 1x10⁻⁹s

A = area = 1 mm² = 1x10⁻⁶m²

Question: What energy does it deliver, E = ?

First, you need to calculate the intensity of the wave:

`I=(c\epsilon *E_(m)^(2) )/(2)`

Here

c = speed of light = 3x10⁸m/s

ε = permittivity = 8.85x10⁻¹²C²/N m²

Substituting:

`I=(3x10^(8)*8.85x10^(-12)*(2.09x10^(11))^(2) )/(2) =5.799x10^(19)W/m^(2)`

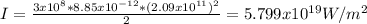
The energy:

`E=IAt=5.799x10^(19)*1x10^(-6)*1x10^(-9)=5.799x10^(4)J`