Answer:
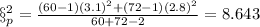
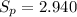

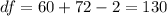
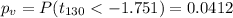
Assuming a significance level of
 we have that the p value is lower than this significance level so then we can conclude that the mean for checkout time is significantly less for people who use the self-service lane
we have that the p value is lower than this significance level so then we can conclude that the mean for checkout time is significantly less for people who use the self-service lane
Explanation:
Data given
Our notation on this case :
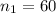 represent the sample size for people who used a self service
represent the sample size for people who used a self service
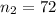 represent the sample size for people who used a cashier
represent the sample size for people who used a cashier
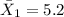 represent the sample mean for people who used a self service
represent the sample mean for people who used a self service
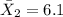 represent the sample mean people who used a cashier
represent the sample mean people who used a cashier
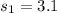 represent the sample standard deviation for people who used a self service
represent the sample standard deviation for people who used a self service
 represent the sample standard deviation for people who used a cashier
represent the sample standard deviation for people who used a cashier
Assumptions
When we have two independent samples from two normal distributions with equal variances we are assuming that

The statistic is given by:
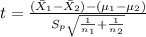
And t follows a t distribution with
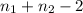 degrees of freedom and the pooled variance
degrees of freedom and the pooled variance
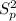 is given by this formula:
is given by this formula:
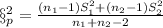
System of hypothesis
Null hypothesis:

Alternative hypothesis:
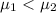
This system is equivalent to:
Null hypothesis:
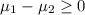
Alternative hypothesis:

We can find the pooled variance:
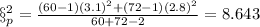
And the deviation would be just the square root of the variance:
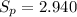
The statistic is given by:

The degrees of freedom are given by:
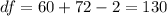
And now we can calculate the p value with:
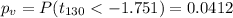
Assuming a significance level of
 we have that the p value is lower than this significance level so then we can conclude that the mean for checkout time is significantly less for people who use the self-service lane
we have that the p value is lower than this significance level so then we can conclude that the mean for checkout time is significantly less for people who use the self-service lane