Answer:
109 Employees
Explanation:
Total Number of Employees, Universal Set=128
Key: P=Climb poles, T=Cut down trees, W=Splice wire
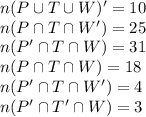
Since 9 can do exactly one of the three.
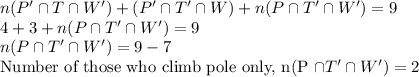
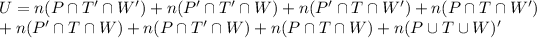
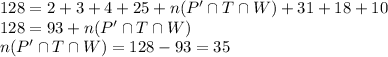
Number of Employees who can do at least two of the jobs
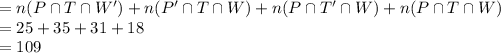
109 Employees can do at least two of the jobs.
OR
- 9 can do exactly one job
- 10 cannot do any one of the jobs
Therefore: Number who can do at least two jobs
=128-(10+9)=109