Answer:
(c)
"The given statement is true, by definition of length of a vector
 ,
,
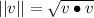 "
"
Explanation:
(a)
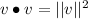
That is completely correct Remember that if
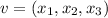 then
then
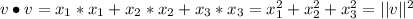
Therefore the correct answer would be (c).
"The given statement is true, by definition of length of a vector
 ,
,
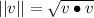 "
"