Question

An engineer wants to design an oval racetrack such that 1.424 x 104 N race cars can round the exactly 304.9 m radius turns at 45.6 m/s without the aid of friction. She estimates that the cars will round the turns at a maximum of 78.2 m/s. Find the banking angle θ necessary for the race cars to navigate the turns at 45.6 m/s without the aid of friction.

Answer 1

The banking angle required is
`55.7^(0)`.

Step-by-step explanation:

Banking of a road is the act of constructing a road along a curved path at a certain angle to avoid skidding-off of vehicles plying it. Centripetal force is required to pull the object moving with a velocity 'v' towards the center of the curve for stability.

The velocity of a car navigating a banked road is given by:

v =
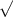`√( )`(rg ÷ tanθ)

where: r is the radius of the road, g is the gravitational force and θ is the banking angle.

⇒
`v^(2)` = rg ÷ tanθ

tanθ =
`(rg)/(v^(2) )`

θ =
`tan^(-1)`
`(rg)/(v^(2) )`

=
`tan^(-1)`
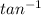
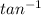
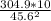`(304.9 * 10)/(45.6^(2) )` (given that g = 10
`ms^(-2)`)

=
`tan^(-1)`
`(3049)/(2079.36)`

=
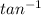
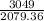
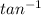`tan^(-1)` 1.4663

θ =
`55.7^(0)`

The banking angle required is
`55.7^(0)`.