Answer:
693 Years
Explanation:
Given an initial amount
 and k (a negative constant) determined by the nature of the material, the amount of radioactive material remaining at a given time t, is determined using he formula:
and k (a negative constant) determined by the nature of the material, the amount of radioactive material remaining at a given time t, is determined using he formula:
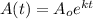
If a certain radioactive isotope decays at a rate of 0.1% annually.
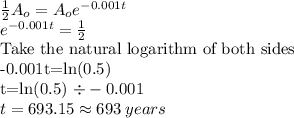
The half-life of the isotope is 693 years.