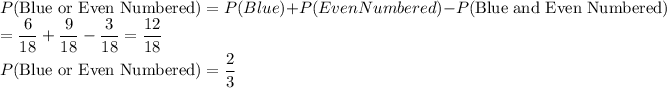Question

A jar contains 12 red marbles numbered 1 to 12 and 6 blue marbles numbered 1 to 6. A marble is drawn at random from the jar. Find the probability of the given event, please show your answers as reduced fractions. (a) The marble is red. P(red)= (b) The marble is odd-numbered. P(odd)= (c) The marble is red or odd-numbered. P(red or odd) = (d) The marble is blue or even-numbered. P(blue or even) = Question Help: Forum Post to forum Submit Question

Answer 1

`(a)P(Red)=(2)/(3)\\(b)P(Odd) =(1)/(2)\\(c)P(\text{Red or Odd Numbered})=(5)/(6)\\(d)P(\text{Blue or Even Numbered})=(2)/(3)`

Explanation:

Number of Red Marbles{1,2,3,4,5,6,7,8,9,10,11,12},n(R)=12

Number of Blue Marbles{1,2,3,4,5,6},n(B)=6

Total Number of Marbles, n(S)=6+12=18

(a)Probability that the Marble is Red

`P(R)=(n(R))/(n(S)) =(12)/(18) =(2)/(3)`

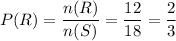
(b)Probability that the marble is odd-numbered.

Number of Odd-Numbered Balls, n(O)=9

`P(Odd)=(n(O))/(n(S)) =(9)/(18) =(1)/(2)`

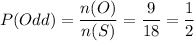
(c)Probability that the marble is red or odd-numbered.

n(Red)=12

n(Odd Numbered marbles)=9

n(Red and Odd Numbered Marbles)=6

`P(\text{Red or Odd Numbered})=P(Red)+P(Odd\:Numbered)-P(\text{Red and Odd Numbered)}\\=(12)/(18) +(9)/(18)-(6)/(18) =(15)/(18)\\P(\text{Red or Odd Numbered})=(5)/(6)`(d)Probability that the marble is blue or even-numbered.

n(Blue)=6

n(Even Numbered marbles)=9

n(Blue and Even Numbered Marbles)=3

`P(\text{Blue or Even Numbered})=P(Blue)+P(Even\:Numbered)-P(\text{Blue and Even Numbered)}\\=(6)/(18) +(9)/(18)-(3)/(18) =(12)/(18)\\P(\text{Blue or Even Numbered})=(2)/(3)`