Question

Calibrating a scale:

Making sure that the scales used by businesses in the United States are accurate is the responsibility of the National Institute for Standards and Technology (NIST) in Washington, D.C. Suppose that NIST technicians are testing a scale by using a weight known to weigh exactly 1000 grams. The standard deviation for scale reading is known to be σ = 2.3. They weigh this weight on the scale 49 times and read the result each time. The 49 scale readings have a sample mean of x = 999.0 grams. The calibration point is set too low if the mean scale reading is less than 1000 grams.
1. The technicians want to perform a hypothesis test to determine whether the calibration point is set too low. Use the α = 0.01 level of significance and the P-value method with the TI-84 calculator.

Answer 1

We conclude that the calibration point is set too low.

Explanation:

We are given that NIST technicians are testing a scale by using a weight known to weigh exactly 1000 grams. The standard deviation for scale reading is known to be σ = 2.3. They weigh this weight on the scale 49 times and read the result each time. The 49 scale readings have a sample mean of x = 999.0 grams.

The calibration point is set too low if the mean scale reading is less than 1000 grams.

Let
`\mu` = mean scale reading

So, Null Hypothesis,
`H_0` :
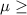`\mu \geq` 1000 grams {means that the calibration point is not set too low}

Alternate Hypothesis,
`H_A` :
`\mu` < 1000 grams {means that the calibration point is set too low}

The test statistics that would be used here One-sample z test statistics as we know about the population standard deviation;

T.S. =
`(\bar X-\mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

where,
`\bar X` = sample mean = 999 grams

`\sigma` = population standard deviation = 2.3 grams

n = sample of scale readings = 49

So, test statistics =
`(999-1000)/((2.3)/(√(49) ) )`

= -3.04

The value of z test statistics is -3.04.

Now, P-value of the test statistics is given by the following formula;

P-value = P(Z < -3.04) = 1 - P(Z
`\leq` 3.04)

= 1 - 0.99882 = 0.00118

Since, the P-value is less than the level of significance as 0.01 > 0.00118, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region.

Therefore, we conclude that the calibration point is set too low.