Answer:
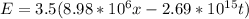
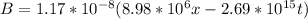
Step-by-step explanation:
The electric field equation of a electromagnetic wave is given by:
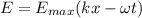 (1)
(1)
- E(max) is the maximun value of E, it means the amplitude of the wave.
- k is the wave number
- ω is the angular frequency
We know that the wave length is λ = 700 nm and the peak electric field magnitude of 3.5 V/m, this value is correspond a E(max).
By definition:

![k=8.98*10^(6) [rad/m]](https://img.qammunity.org/2021/formulas/physics/college/18nwdxgcggbjv2icfnq46iqs658kq7wgqw.png)
And the relation between λ and f is:
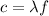
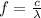
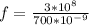
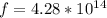
The angular frequency equation is:
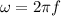
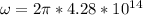
![\omega=2.69*10^(15) [rad/s]](https://img.qammunity.org/2021/formulas/physics/college/lg04b31ghnuilz1x02igyybc3la81sn8r1.png)
Therefore, the E equation, suing (1), will be:
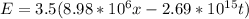 (2)
(2)
For the magnetic field we have the next equation:
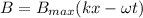 (3)
(3)
It is the same as E. Here we just need to find B(max).
We can use this equation:

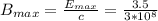
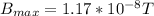
Putting this in (3), finally we will have:
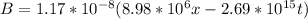 (4)
(4)
I hope it helps you!