1 Answer

Vedha Peri · Answer 1 · 2021-07-06T01:54:28+0000

Answer:

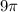$9\pi$ sq. units.

Explanation:

It is given that a circle has a sector with area
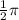$(1)/(2)\pi$ and central angle of
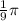$(1)/(9)\pi$ radians.

We know that, the area of sector is

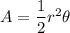
$A=(1)/(2)r^2\theta$

where, r is radius and
$\theta$ is central angle in radian.

Substitute the values of A and
$\theta$ .

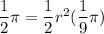
$(1)/(2)\pi=(1)/(2)r^2((1)/(9)\pi)$

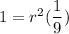
1=r^2((1)/(9))

9=r^2

3=r

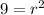
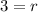
The radius of the circle is 3 units.

So, the area of circle is

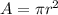
$A=\pi r^2$

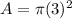
$A=\pi (3)^2$

$A=9\pi$

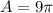
Therefore, the area of circle is
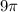$9\pi$ sq. units.

Please log in or register to add a comment.