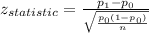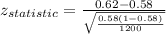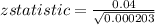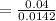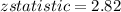Question

In a test of hypothesis, the null hypothesis is that the population proportion is equal to .58 and the alternative hypothesis is that the population proportion is greater than .58. Suppose we make the test at the 2.5% significance level. A sample of 1200 elements selected from this population produces a sample proportion of .62. What is the value of the test statistic, z?

Answer 1

z statistic = 2.82

Explanation:

Sample size = 1200

Null hypothesis,
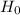`H_(0)`: p = 0.58

Alternative hypothesis,
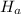`H_(a)`: p > 0.58

From the null and alternative hypothesis, we can derive that Hypothesized proportion,
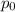`p_(0)` = 0.58 = 58%

Significance level = 2.5% = 0.025

Sample proportion,
`p_(1)` = 0.62 = 62%

Test statistic, z:

`z_(statistic) = \frac{p_(1) -p_(0) }{\sqrt{(p_(0)( 1 -p_(0) ))/(n) } }`

`z_(statistic) = \frac{0.62-0.58}{\sqrt{(0.58(1-0.58))/(1200) } }`

`z statistic =(0.04)/(√(0.000203) )`
`= (0.04)/(0.0142)`

`z statistic = 2.82`