Question

Steroids, which are dangerous, are sometimes used to improve athletic performance. A study by the National Athletic Trainers Association surveyed random samples of 1679 high school freshmen and 1366 high school seniors in Illinois. Results showed that 34 of the freshmen and 24 of the seniors had used anabolic steroids. Estimate at a 95% confidence level the difference between the proportion of freshmen using steroids in Illinois and the proportion of seniors using steroids in Illinois.

Answer 1

At 95% confidence level, the difference between the proportion of freshmen using steroids in Illinois and the proportion of seniors using steroids in Illinois is -7.01135×10⁻³ <
`\hat{p}_1-\hat{p}_2` < 1.237

Explanation:

Here we are required to construct the 95% confidence interval of the difference between two proportions

The formula for the confidence interval of the difference between two proportions is as follows;

`\hat{p}_1-\hat{p}_2\pm z^(*)\sqrt{\frac{\hat{p}_1\left (1-\hat{p}_1 \right )}{n_(1)}+\frac{\hat{p}_2\left (1-\hat{p}_2 \right )}{n_(2)}}`

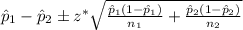
Where:

`\hat{p}_1 = (34)/(1679)`

`\hat{p}_2 = (24)/(1366)`

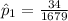
n₁ = 1679

n₂ = 1366

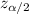`z_(\alpha /2)` at 95% confidence level = 1.96

Plugging in the values, we have;

`(34)/(1679)- (24)/(1366) \pm 1.96 * \sqrt{( (34)/(1679)\left (1- (34)/(1679)\right ))/(1679)+((24)/(1366) \left (1-(24)/(1366) \right ))/(1366)}`

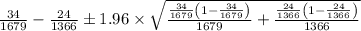
Which gives;

-7.01135×10⁻³ <
`\hat{p}_1-\hat{p}_2` < 1.237.

At 95% confidence level, the difference between the proportion of freshmen using steroids in Illinois and the proportion of seniors using steroids in Illinois = -7.01135×10⁻³ <
`\hat{p}_1-\hat{p}_2` < 1.237.