Given Information:
Young adults who received help from parents = 8
Total number of young adults = 40
Confidence level = 95%
Required Information:
Margin of error = ?
95% confidence interval = ?
Answer:
Margin of error = 0.124
95% Confidence Interval = (0.076, 0.324)
Explanation:
The proportion of young adults who purchased a home in Kentucky and received help from their parents is given by
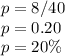
The margin of error is given by
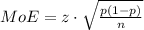
Where p is the proportion of young adults who purchased a home in Kentucky and received help from their parents and n is the total number of young adults.
The z-score corresponding to 95% confidence level is 1.96

Whereas the confidence interval is given by
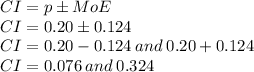
Therefore, we are 95% Confident that the young adults who purchased a home in Kentucky and received help from their parents is within the Interval of (0.076, 0.324)