Question

In the given figure, mWY = 76° and mXZ = 112. What is the difference of the measures of angle WPY and angle XPY?

Answer 1

the answer is A 8 degrees.

Explanation:

I just took this test on edmentum.

Answer 2

Please consider the attached image for complete question.

We have been given that measure of arc WY is 76° and and measure of arc XZ is 112°. We are asked to find the difference of of the measures of angle WPY and angle XPY.

First of all we will find the measure of angle WPY using intersecting secants theorem. Intersecting secants theorem states that measure of angle formed by two intersecting secants inside a circle is half the sum of intercepting arcs.

`m\angle WPY=(1)/(2)(\widehat{WY}+\widehat{XZ})`

`m\angle WPY=(1)/(2)(76^(\circ)+112^(\circ))`

`m\angle WPY=(1)/(2)(188^(\circ))`

`m\angle WPY=94^(\circ)`

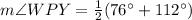
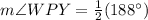
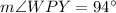
We can see that angle WPY and angle XPY are linear angles, so they will add up-to 180 degrees.

`m\angle WPY+m\angle XPY=180^(\circ)`

`94^(\circ)+m\angle XPY=180^(\circ)`

`94^(\circ)-94^(\circ)+m\angle XPY=180^(\circ)-94^(\circ)`

`m\angle XPY=86^(\circ)`

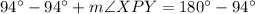
Now we need to find difference of both angles as:

`m\angle WPY-m\angle XPY=94^(\circ)-86^(\circ)`

`m\angle WPY-m\angle XPY=8^(\circ)`

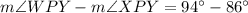
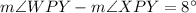
Therefore, the difference of the measures of angle WPY and angle XPY is 8 degrees.