Question

Suppose small aircraft arrive at a certain airport according to a Poisson process with rate α = 8 per hour, so that the number of arrivals during a time period of t hours is a Poisson rv with parameter μ = 8t. (Round your answers to three decimal places.) (a) What is the probability that exactly 9 small aircraft arrive during a 1-hour period?

Answer 1

0.124 = 12.4% probability that exactly 9 small aircraft arrive during a 1-hour period.

Explanation:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

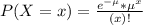
In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given time interval.

Rate of 8 per hour

This means that
`\mu = 8`

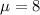
(a) What is the probability that exactly 9 small aircraft arrive during a 1-hour period?

This is P(X = 9).

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 9) = (e^(-8)*8^(9))/((9)!) = 0.124`

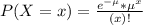
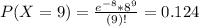
0.124 = 12.4% probability that exactly 9 small aircraft arrive during a 1-hour period.