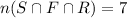Question

A total of 1 232 students have taken a course in Spanish, 879 have taken a course in French, and 114 have taken a course in Russian. Further, 103 have taken courses in both Spanish and French, 23 have taken courses in both Spanish and Russian, and 14 have taken courses in both French and Russian. If 2 092 students have taken at least one of Spanish, French, and Russian, how many students have taken a course in all three languages

Answer 1

`n(S\cap F \cap R)=7`

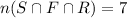
Explanation:

The Universal Set, n(U)=2092

`n(S)=1232\\n(F)=879\\n(R)=114`

`n(S\cap R)=23\\n(S\cap F)=103\\n(F\cap R)=14`

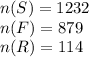
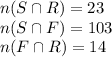
Let the number who take all three subjects,
`n(S\cap F \cap R)=x`

Note that in the Venn Diagram, we have subtracted
`n(S\cap F \cap R)=x` from each of the intersection of two sets.

The next step is to determine the number of students who study only each of the courses.

`n(S\:only)=1232-[103-x+x+23-x]=1106+x\\n(F\: only)=879-[103-x+x+14-x]=762+x\\n(R\:only)=114-[23-x+x+14-x]=77+x`

These values are substituted in the second Venn diagram

Adding up all the values

2092=[1106+x]+[103-x]+x+[23-x]+[762+x]+[14-x]+[77+x]

2092=2085+x

x=2092-2085

x=7

The number of students who have taken courses in all three subjects,
`n(S\cap F \cap R)=7`