Question

Find the 72nd term of the arithmetic sequence 11, 7,3,...​

Answer 1

3124

Explanation:

Answer 2

Answer: -273

Step-by-step explanation: To determine the 72nd term, we will want use our explicit formula which is shown below.

`^(a)n = ^(a)1 + (n - 1)d`

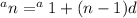
Since we want to find the 72nd term, the
`^(a)n`

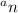
in the formula will be changed to
`^(a) 72`.

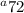Also, the 72 will be substituted in for the n

that is inside the set of parentheses.

Then
`^(a) 1` will be the 1st term given in our sequence or 11.

Lastly, the d outside the parentheses is the difference between

each of the terms in the sequence which is -4.

So we now have
`^(a) 72 = 11 + (72 - 1)(-4)`.

Now we have all the information we need.

Now we can simplify from here.

Make sure to apply your order of operations because

this is where a lot of students make mistake.

Start simplifying inside the parentheses!

(72 - 1) is going to be 70.

So we have
`^(a) 72 = 11 + (71)(-4)`.

Then, we have to multiply before we add.

So (71)(-4) is going to be -284.

So we have
`^(a) 72 = 11 + (-284)`.

Solving from here, 11 + (-284) simplifies to -273.

This means that the 72nd term of this sequence is -273.