Answer:
120 m
Step-by-step explanation:
Given:
wavelength 'λ' = 2.4m
pulse width 'τ'= 100T ('T' is the time of one oscillation)
The below inequality express the range of distances to an object that radar can detect
τc/2 < x < Tc/2 ---->eq(1)
Where, τc/2 is the shortest distance
First we'll calculate Frequency 'f' in order to determine time of one oscillation 'T'
f = c/λ (c= speed of light i.e 3 x
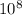 m/s)
m/s)
f= 3 x
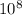 / 2.4
/ 2.4
f=1.25 x
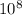 hz.
hz.
As, T= 1/f
time of one oscillation T= 1/1.25 x
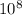
T= 8 x
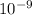 s
s
It was given that pulse width 'τ'= 100T
τ= 100 x 8 x
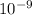 => 800 x
=> 800 x
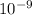 s
s
From eq(1), we can conclude that the shortest distance to an object that this radar can detect:
 = τc/2 => (800 x
= τc/2 => (800 x
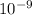 x 3 x
x 3 x
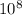 )/2
)/2
 =120m
=120m