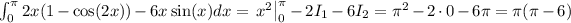Question

Use​ Green's Theorem to evaluate the following line integral. Assume the curve is oriented counterclockwise The circulation line integral of Fequalsleft angle 4 xy squared comma 2 x cubed plus y right angle where C is the boundary of StartSet (x comma y ): 0 less than or equals y less than or equals sine x comma 0 less than or equals x less than or equals pi EndSet

Answer 1

The answer is
`\pi(\pi-6)`

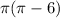
Explanation:

Recall that green theorem is as follows: Given a field F(x,y) = (P(x,y),Q(x,y)) and a closed curve C that is counterclockwise oriented. If P and Q are continuosly differentiable, then

`\oint_C F\cdot dr = \int_(R) (\partial P )/(\partial y)-(\partial P )/(\partial x) dA`

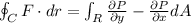
where R is the region enclosed by the curve C.

In this particular case, we have the following field
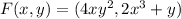`F(x,y) = (4xy^2,2x^3+y)`. We are given the description of the region R as
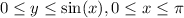`0\leq y \leq \sin(x), 0\leq x \leq \pi`. So, in this case (calculations are omitted)

`(\partial P)/(\partial y) = 8xy, (\partial Q)/(\partial x) = 6x`

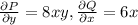
Thus,

`\oint_C F\cdot dr =\int_(0)^(\pi)\int_(0)^(\sin(x))(8xy-6x)dydx`

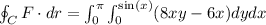
So,

`\int_(0)^(\pi)\int_(0)^(\sin(x))(8xy-6x)dydx=\int_(0)^(\pi)4x\left.y^2\right|_(0)^(\sin(x))-6x\left.y\right|_(0)^(\sin(x)) = \int_(0)^(\pi) 4x\sin^2(x)-6x\sin(x)dx`

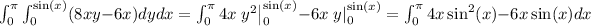
Since
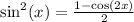`\sin^2(x) = (1-\cos(2x))/(2)`, then

`\int_(0)^(\pi) 4x\sin^2(x)-6x\sin(x)dx = \int_(0)^(\pi) 2x(1-\cos(2x))-6x\sin(x)dx`

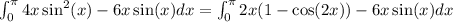
Consider the integrals

`I_1 = \int_(0)^(\pi) x\cos(2x)dx, I_2 = \int_(0)^(\pi)x\sin(x)dx`

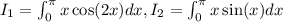
Then, by using integration by parts (whose calculations are omitted) we get

`\int_(0)^(\pi) x\cos(2x) = \left.(x\sin(2x))/(2)+(\cos(2x))/(4)\right|_(0)^(\pi) = (\pi\sin(2\pi))/(2)+(\cos(2\pi))/(4)- (0\sin(2\cdot 0))/(2)+(\cos(2\cdot 0))/(4)=0`

`\int_(0)^(\pi)x\sin(x) = \left.-x\cos(x)+\sen(x)\right |_(0)^(\pi) = -\pi\cos(\pi)+\sen(\pi)- (-0\cdot \cos(\pi)+\sin(0)) = \pi`

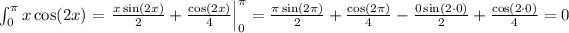
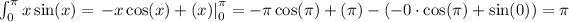
Then, we have that

`\int_(0)^(\pi) 2x(1-\cos(2x))-6x\sin(x)dx = \left.x^2\right|_(0)^(\pi) -2I_1-6I_2 = \pi^2-2\cdot 0 -6\pi = \pi(\pi-6)`