Question

For a standard normal distribution, find the approximate value of P(z≤0.42). Use the portion of the standard normal table below to help answer the question.

0.00
0.22
0.32
0.42
0.44
0.64
0.84
1.00
Probability
0.5000
0.5871
0.6255
0.6628
0.6700
0.7389
0.7995
0.8413
O
A. 16%
B. 34%
C. 66%
D. 84%​

Answer 1

C

Explanation:

Answer 2

We have been given that a z-score table and corresponding probability to each z-score. We are asked to find the probability of a getting a z-score less than or equal to 0.42 that is
`P(z\leq0.42)`.

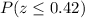z-score Probability

0.00 0.5000

0.22 0.5871

0.32 0.6255

0.42 0.6628

0.44 0.6700

0.64 0.7389

0.84 0.7995

1.00 0.8413

Upon looking at our given table, we can see that the probability corresponding to z-score of 0.42 is 0.6628.

`P(z\leq0.42)=0.6628`

Now, we will convert
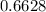`0.6628` into percent as:

`0.6628* 100\%=66.28\%`

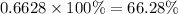
Upon rounding to nearest percent, we will get:

`66.28\%\approx 66\%`

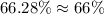
Therefore, the approximate value of
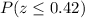`P(z\leq0.42)` is
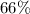`66\%` and option C is the correct choice.