Question

What are rational. numbers?

Answer 1

Rational numbers are numbers that can be expressed as a quotient or fraction, written in p\q form, where q cannot equal 0. Example would be 2/5, 1/3, 9/3.

Answer 2

Rational numbers are defined as "a number that can be expressed as the quotient or fraction p/q of two integers, a numerator p and a non-zero denominator q." This quote can be broken down to make it easier to understand. In basic terms, a rational number is a real number that is an integer, fraction, terminating decimal, or repeating decimal.

Integer

An integer is any positive or negative whole number including 0. Examples of integers include 4, -9, and 0.

Fraction

All fractions that do not have a 0 denominator (which makes the number undefined) are rational numbers. Additionally, complex fractions are not always considered rational numbers. Complex fractions are fractions where either the numerator or denominator is a decimal or fraction itself. Examples of rational fractions include
`\frac{4}5}`,
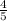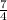`(7)/(4)`, and
`(2)/(2)`.

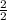Terminating Decimals

Terminating decimals are decimals that have a finite number of digits. This means that the decimal stops at some point. Examples of terminating decimals include 0.346, 0.47834, and 0.345832454525456

Repeating Decimals

Repeating decimals are any decimal that is not terminating but has some pattern that repeats for infinity. Examples of repeating decimals include
`0.\bar 9`,
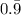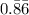`0.\bar8\bar6`, and
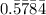`0.\bar 5\bar7\bar8\bar4`. In this case, the bar notation represents numbers that repeat forever.