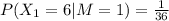Answer:
Explanation:
The pairs of the Outcome from the two dice
 are given below:
are given below:
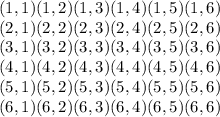
Given
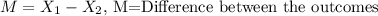 , the sample space of M is:
, the sample space of M is:

(a)Probability that M is negative
n(Negative Terms)=15
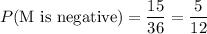
(b)Probability that M is positive
n(Positive Terms)=15
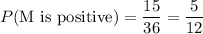
(c)Probability that M=0
n(Zeroes)=6
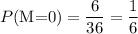
(d) n(M=6)=0
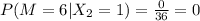
(e)If M=1, the probability that
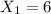
When
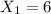 , the number of outcomes where M=1 is 1.
, the number of outcomes where M=1 is 1.
Therefore: