Question

g You shine a laser on a plastic prism made from an unknown material and measure the angles relative to the normal that the light takes both inside and outside the medium. You make a plot of sin θinside versus sin θoutside for the plastic object and calculate the slope of best-fit line of your plot to be 0.79365 ± 0.05669. What is the index of refraction of the plastic object?

Answer 1

The refractive index of the plastic, n₂ is between 0.73696 and 0.85034

Step-by-step explanation:

Here we have;

Snell's law which is the relationship of the refractive index of light in two media. The law, in mathematical terms, states the ratio of the refractive index of light between two media is inversely proportional to the ratio of the sine of the angle of incidence to the sine of the angle of refraction.

That is the sine of the angle of incidence and the sine of the angle of refraction are inversely proportional.

`(n_1)/(n_2) = (sin \theta_2)/(sin \theta_1)`

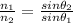
0.79365 ± 0.05669

If θ₂ = Angle inside the plastic object and

θ₁ = Angle outside the plastic object

n₁ = Refractive index of air outside the plastic = 1

n₂ = Refractive index of the plastic

Therefore,
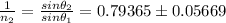`(1)/(n_2) = (sin \theta_2)/(sin \theta_1) = 0.79365 \pm 0.05669`, which gives;

`n_2 = (1)/(0.79365 \pm 0.05669)`

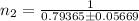
∴ 0.73696 ≤ n₂ ≤ 0.85034.

The refractive index of the plastic, n₂ is between 0.73696 and 0.85034.