Answer:
a)
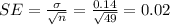
b)

c)
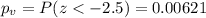
d) Null hypothesis:
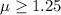
Alternative hypothesis:
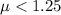
e) For this case we need to find a critical value who accumulate 0.05 of the area in the left at the normal standard distribution and we got:
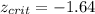
Since our calculated value is lower than the critical value we have enough evidence to reject the null hypothesis at the significance level provided of 5%
f)
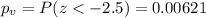
Since the p value is lower than the significance level we have enough evidence to reject the null hypothesis at 5% of significance. Same result with the critical value approach.
Explanation:
For this case we want to test is the true mean for the gasoline prices are significantly reduced from $1.25 per liter, so then the system of hypothesis are:
Null hypothesis:
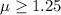
Alternative hypothesis:
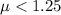
Part a
The standard error for this case is given by:
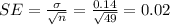
Part b
The statistic for this hypothesis is given by:
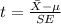
And replacing the info provided we got:

Part c
Since we are conducting a left tailed test the p value would be given by:
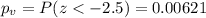
And we can use the following excel code to find it:
=NORM.DIST(-2.5,0,1,TRUE)
Part d
Null hypothesis:
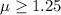
Alternative hypothesis:
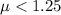
Part e
For this case we need to find a critical value who accumulate 0.05 of the area in the left at the normal standard distribution and we got:
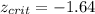
Since our calculated value is lower than the critical value we have enough evidence to reject the null hypothesis at the significance level provided of 5%
Part f
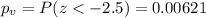
Since the p value is lower than the significance level we have enough evidence to reject the null hypothesis at 5% of significance. Same result with the critical value approach.