Answer:
The replacing the grass will cost Mr. Ishimoto $14.00.
Explanation:
The area of a rectangular field is:
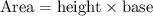
It is provided that Mr. Ishimoto needs to replace the grass in the section of his lawn.
The grass section can be broken into 2 rectangles.
First rectangle: Base = 7 feet and Height = 3 feet.
Second rectangle: Base = 2 feet and Height = 7 feet.
Compute the area of both the rectangles as follows:
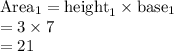
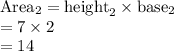
Now the cost of the new grass is $0.40 per square foot.
Compute the cost of replacing the grass in the first rectangular section as follows:

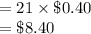
Compute the cost of replacing the grass in the second rectangular section as follows:


The total cost of replacing the grass is:
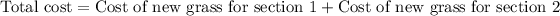
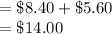
Thus, the replacing the grass will cost Mr. Ishimoto $14.00.