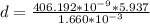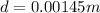Answer:
The spacing between the slits is
Step-by-step explanation:
From the question we are told that
The wavelength of the light is
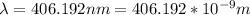
The distance of the slit from the screen is
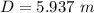
The number of bright fringe is
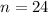
The length the fringes span is
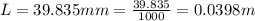
The fringe width (i.e the distance of between two successive bright or dark fringe) is mathematically represented as
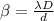
Where d is the distance between the slits
 is the fringe width which can also be evaluated as
is the fringe width which can also be evaluated as
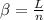
Substituting values

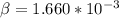
Making d the subject of formula in the above equation
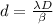
Substituting values